Demystifying Portfolio Optimization with Python and CVXOPT
Do you want to do fast and easy portfolio optimization with Python? Then CVXOPT, and this post, are for you! Here’s a gentle intro to portfolio theory and some code to get you started.
Gold has been performing well in the Covid-19 market, rising close to $2000/oz. before trading recently around $1700. Should long-term investors have gold in their portfolio, and how much?
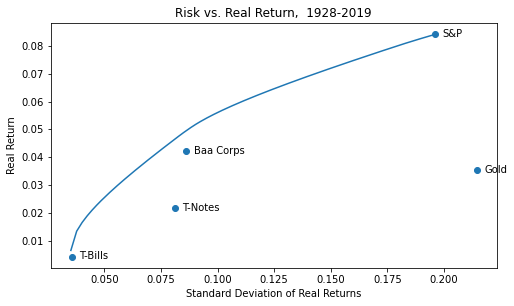
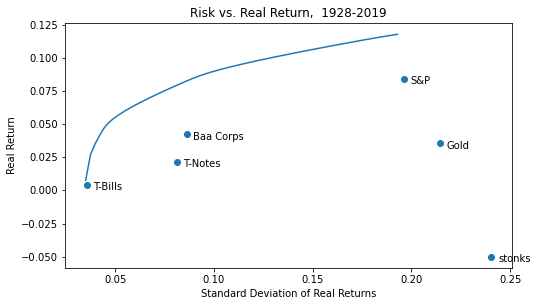
One way to answer this question is to look at how portfolios with and without gold performed. Using a portfolio optimization framework, we can find the highest-return portfolio for any feasible level of risk: the classic efficient frontier above.
For each asset, the marker represents the historical mean real return (y-axis) vs. the historical standard deviation of real returns (x-axis). The line represents the return and risk for optimal combinations of these 5 assets that maximize the return for that level of risk (or vice versa, minimize the level of risk for a specified threshold return). The efficient frontier line slopes upward, because the more risk you take, the more return you should get. More to the point, if it sloped down, that would mean you accepted more risk for less return, which by our definition would not be an optimal combination.
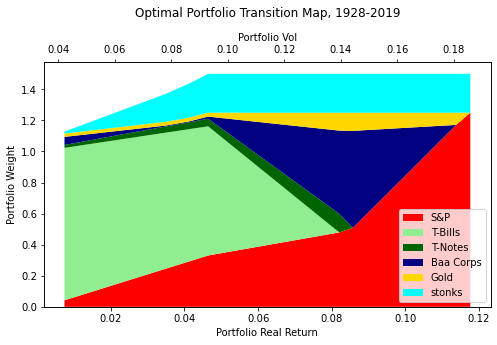
By looking at whether optimal portfolios contain gold, and over which time periods and risk levels, we can get a sense of whether we should own gold, and how much. We can plot a transition map of the composition of the portfolio as you move along the efficient frontier:
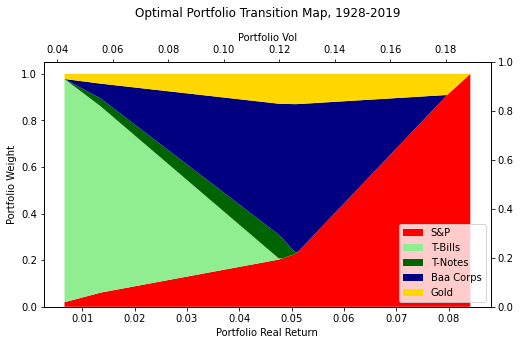
The transition map is a stacked area chart of the composition of the portfolio at each point on the frontier. The leftmost point shows the minimum risk portfolio, with the risk on the top x-axis and the return on the bottom x-axis, and the colors representing each asset in the portfolio. The rightmost point shows the riskiest optimal portfolio, which is 100% stocks. In between, we see the composition of the optimal portfolio as we vary our risk and move along the efficient frontier.
We observe that a small allocation of gold is present in most portfolios, except for the riskiest optimal portfolio. The minimum-volatility portfolio is T-bills plus a little bit of S&P plus a little bit of gold. The highest-volatility portfolio is of course 100% stocks, but if you lower the volatility constraint, the first asset you add is gold.
Next, we’ll take a step back and discuss portfolio theory basics, how we compute the risk, and how we optimize with CVXOPT.
Why do we use the standard deviation of returns as a proxy for risk?
Using Warren Buffet’s analogy, we anthropomorphize the market as a moody partner who co-invests in our stocks, and whose valuation varies with his mood swings. On a good day, Mr. Market values a security according to the best-case scenario: at the high end of the range of potential valuations. On a bad day, he values it according to the worst-case scenario, at the low end of the range.
On a typical day, Mr. Market moves a typical distance between the two extremes of fear and greed. ‘Volatility’ is how much a stock moves on a typical day based on Mr. Market’s mood swings. This distance is a proxy for how wide Mr. Market’s valuation range is, hence how risky the market thinks the security is. See footnote1 for a more mathematical explanation.
As an investor, should you care how the market perceives risk? That depends. First, do you believe the market’s implicit risk perception is worth knowing to inform your own decisions? And even if not, are you going to trade with the market?
If the answer to both questions is ‘no’, then maybe you don’t care about volatility. If you are an omniscient Warren Buffett, with your own deeply-considered valuation of a company, and you want to hold forever, then the daily market price and volatility don’t affect your actions in any way. Risk just means that many futures can unfold but only one future will unfold, even when you know as much as possible. The meaningful measure of risk is the margin of error around your own valuation, due to factors outside your control. You should spend your time thinking about those factors and the margin of error, not the market volatility.
So, if you have confidence in your own risk estimation, the market volatility may be irrelevant to your risk estimate. But if you have to trade with the market, you may still wish to take volatility into account.
Fundamental valuation metrics like price/earnings, price/book, enterprise value/EBITDA are a bit like looking at your poker hand and determining if you have a pair of aces or a pair of unsuited rags. Technical metrics like volatility are a bit like looking at how your opponents have been playing and what their patterns and tells are. Any good poker player will tell you it’s a good idea to pay attention to all of that. (To be honest, in most cases if I had to pick between knowing the value of my hand and knowing how the players will react to my betting, I would pick the latter.)
If you are Warren Buffett, you don’t have to trade, ever. That is a big part of his edge. Market volatility is Buffett’s opportunity. But if you’re planning to retire or might need to sell in the foreseeable future, you should have a feel for volatility. Otherwise, you end up trading at an inopportune time, and worst of all, getting thrown off your game by unforeseen volatility.
Just like historical P/Es, historical volatilities are a tool for investing judgment, not a substitute for it. But most of us aren’t Warren Buffett and are students of the markets. Understanding volatility and risk are part of our journey. Maybe one day I’ll stop caring about portfolio volatility, but today is not that day.
How do you compute portfolio volatility from individual asset volatilities?
Given the historical volatility of each of our assets, how do we compute the volatility of our portfolio?
Of course, we can compute all the historical asset-weighted returns of the portfolio and then compute the standard deviation. But if we want to do optimization we need an expression to optimize, we need to understand how portfolio volatility is determined.
Suppose you own 1 share of asset \(a_1\) and 1 share of asset \(a_2\). And you know the standard deviation of \(a_1\)’s absolute returns \(\sigma_{1}=\) $3 and the standard deviation of \(a_2\)’s absolute returns \(\sigma_{2} =\) $4. What is the volatility of a portfolio with one share of each?
To compute the portfolio return SD, the correlation \(\rho\) (rho) between \(a_1\) and \(a_2\) comes into play, because you need to know if the assets generally move in the same direction or in opposite directions. The correlation is how many SDs we expect \(a_1\)’s return to move from its mean when \(a_2\)’s return moves 1 SD from its mean, and vice versa.
The expression for the risk of the combined portfolio of \(a_1\) and \(a_2\) is:
\[\sigma_{port} = \sqrt{\sigma_{1}^2 + \sigma_{2}^2 + 2 \cdot \rho \cdot \sigma_{1} \cdot \sigma_{2} }\]| Return vol \(\sigma_{1}\) | Return vol \(\sigma_{2}\) | Return correlation \(\rho_{12}\) | Portfolio volatility |
|---|---|---|---|
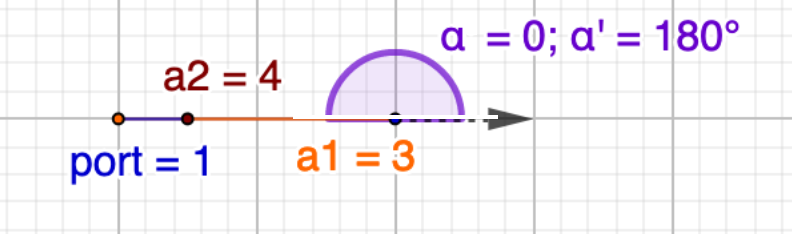
| $3 | $4 | 1.0 | \(\sqrt{3^2 + 4^2 + 2 \cdot 3 \cdot 4 \cdot 1} = 3 + 4 = $7\) |
| $3 | $4 | -1.0 | \(\sqrt{3^2 + 4^2 + 2 \cdot 3 \cdot 4 \cdot (-1)} = 4 - 3 = $1\) |
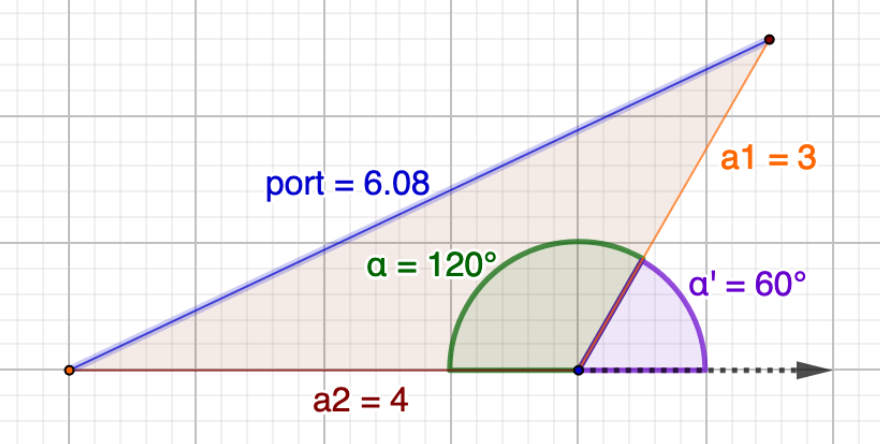
| $3 | $4 | 0.5 | \(\sqrt{3^2 + 4^2 + 2 \cdot 3 \cdot 4 \cdot 0.5} = \sqrt{37} = $6.08\) |
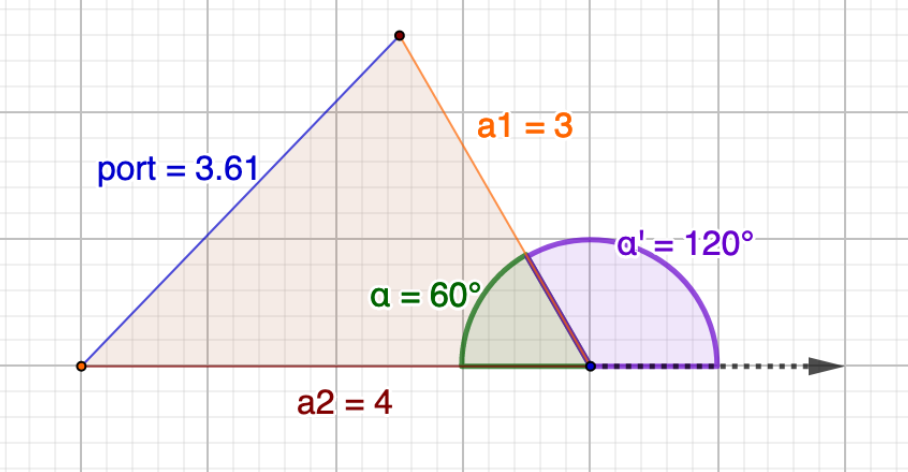
| $3 | $4 | -0.5 | \(\sqrt{3^2 + 4^2 + 2 \cdot 3 \cdot 4 \cdot (-0.5)} = \sqrt{13} = $3.61\) |
| $3 | $4 | 0 | \(\sqrt{3^2 + 4^2} = $5\) |
This should remind you of Pythagoras and square triangles and the cosine rule in trigonometry.
Cosine rule:
\[a = \sqrt{b^2 + c^2 - 2 \cdot cos{\alpha} \cdot b \cdot c }\]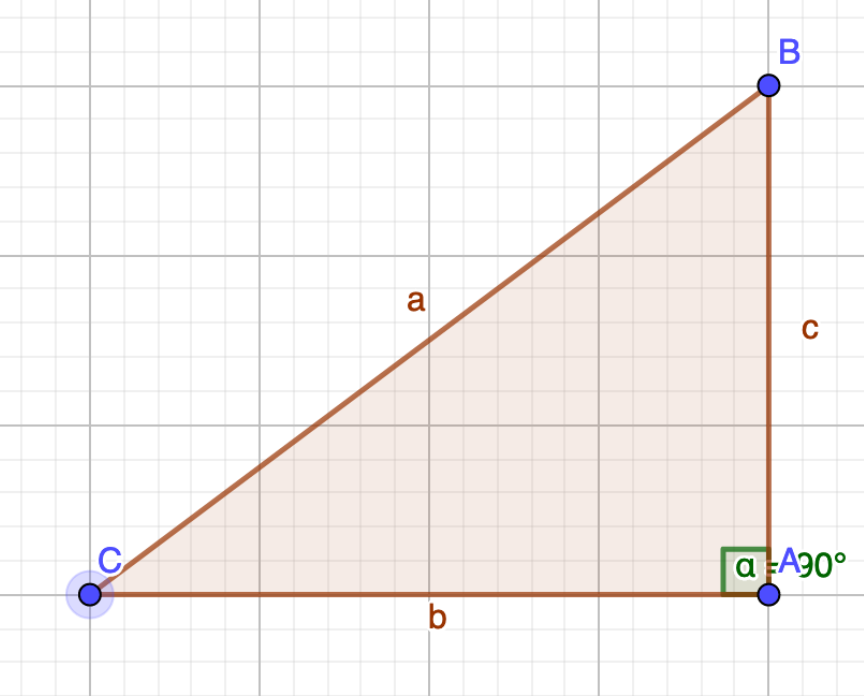
Correlation math is like the cosine rule, but we change the sign of the last term. This gives us a handy way to visualize how correlation and risk interact.
Visualizing risk math geometrically with triangles
- Consider our 2 assets
- Asset \(a_1\) has SD of returns \(\sigma_{1}\)
- Asset \(a_2\) has SD of returns \(\sigma_{2}\)
- \(\rho\) is the correlation between the returns of \(a_1\) and \(a_2\)
- Take the inverse cosine of the correlation. Find the angle \(\alpha' = 180^{\circ} - cos^{-1}\rho\)
- If \(\rho=1, cos^{-1}1 = 0^{\circ}, \alpha'=180^{\circ}\)
- If \(\rho=0, cos^{-1}0 = 90^{\circ}, \alpha' = 180^{\circ} - 90^{\circ} = 90^{\circ}\)
- Make a triangle with 2 sides of length \(\sigma_{1}\) and \(\sigma_{2}\) and the angle \(\alpha'\) between those 2 sides
- The SD of the portfolio returns is given by the length of the third side.
When we plug in angle \(\alpha'\) = 180° - cos-1\(\rho\) in place of \(\alpha\), we reverse the sign of the last term2, and the cosine rule becomes:
\[a = \sqrt{b^2 + c^2 + 2 \cdot cos \alpha' \cdot b \cdot c }\]This matches the risk expression when we use \(\alpha' = 180^\circ - \alpha\).
Examples:
Correlation \(\rho = 0, \alpha' = 90^{\circ}\)
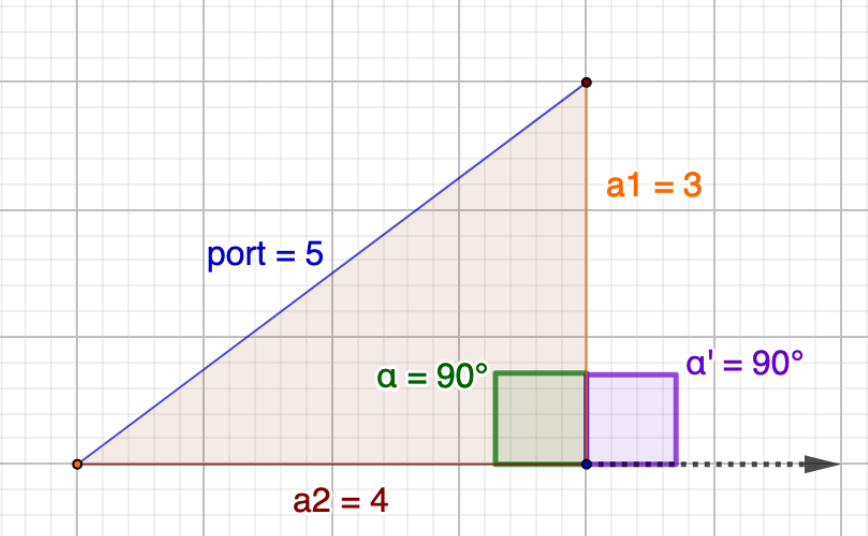
Correlation \(\rho = 0.5, \alpha' = 60^{\circ}\)
Correlation \(\rho = 1.0, \alpha' = 0^{\circ}\)
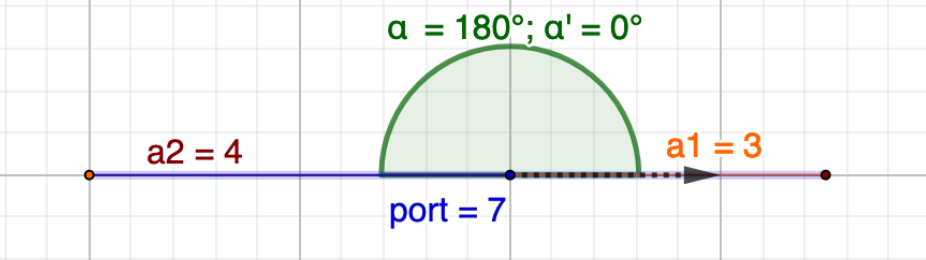
Correlation \(\rho = -1.0, \alpha' = 180^{\circ}\)
Correlation \(\rho = -0.5, \alpha' = 120^{\circ}\)
The covariance matrix, and generalizing to n assets
\(\sigma_{1}\sigma_{2}\rho_{12}\) is the covariance \(\sigma_{12}\). So we can rewrite:
\[\sigma_{port} = \sqrt{\sigma_{1}^2 + \sigma_{2}^2 + 2\sigma_{12}}\]The covariance is the expected value of the product of A’s deviation from its mean and B’s deviation from its mean. The correlation is the covariance scaled by (divided by) the product of A’s standard deviation and B’s standard deviation (the maximum possible covariance if \(\rho=1\)).
The triangles above are drawn assuming 1 share of each asset and absolute dollar returns. To use portfolio weights and percentage returns, we can write the return as:
\[r_{p} = w_{1}r_{1} + w_{2}r_{2}\]and the volatility as:
\[\sigma_{p} = \sqrt{ w_{1}^2\sigma_{1}^2 + w_{2}^2\sigma_{2}^2 + 2w_{1}w_{2}\sigma_{12}}\]\(\sigma_{p}\) is now the volatility in return space instead of absolute space. Generalizing to \(n\) assets and using \(\sigma_{ii}\) to denote the variance of asset \(i\):
\[\sigma_{p} = \sqrt{\sum_{i=1}^{n}\sum_{j=1}^{n}w_{i}w_{j}\sigma_{ij}}\]When you do a nested summation over a square array, you should probably consider a matrix. Define the covariance matrix \(\Sigma\) (using \(\rho=0.5\)) as:
\[\Sigma = \begin{vmatrix} \sigma_{1}^2 & \sigma_{12} \\ \sigma_{21} & \sigma_{2}^2 \end{vmatrix} = \begin{vmatrix} 9 & 6 \\ 6 & 16 \end{vmatrix}\]with variances \(\sigma^2\) on the diagonal and covariances \(\sigma_{ij}\) off the diagonal.
Then we get an elegant matrix notation for the double summation above:
\[\sigma_{p} = \sqrt{\boldsymbol{w^T} \Sigma \boldsymbol{w}}\]Drawing the efficient frontier
What is the efficient frontier? The line describing the set of feasible portfolios a rational investor might choose.
What is the leftmost point on the efficient frontier? It’s the minimum volatility portfolio.
We can find the weights for the minimum volatility portfolio through a convex optimization. When the objective function is convex, there is a global minimum which we can find efficiently by various methods.
CVXPY is a Python modeling framework for convex optimization (paper), by Steven Diamond and Stephen Boyd of Stanford (who wrote a textbook on convex optimization). In the way Pandas is a Python extension for dataframes, CVXPY is a Python extension for describing convex optimization problems.
CVXPY is a little more user-friendly and more performant than scipy.optimize, and CVXPY supports many solvers on the back end, open-source and commercial.
In particular, CVXPY’s parameter abstraction allows solvers to efficiently re-use previous calculations when tracing out an efficient frontier.
The first step is to load some data from Professor Aswath Damodaran’s website into a Pandas dataframe:
data_xls = 'http://www.stern.nyu.edu/~adamodar/pc/datasets/histretSP.xls'
data_sheet = "Returns by year"
# these will change as rows get added on Damodaran website
skiprows = range(17)
skipfooter = 10
download_df = pd.read_excel('http://www.stern.nyu.edu/~adamodar/pc/datasets/histretSP.xls',
sheet_name=data_sheet,
skiprows=skiprows,
skipfooter=skipfooter)
download_df = download_df.set_index('Year')
Similarly we can load data from the FRED economic indicator database:
import pandas_datareader as pdr
# load gold data from FRED API & save copy locally to CSV file
series = ['GOLDAMGBD228NLBM']
gold_download = pdr.data.DataReader(series,
'fred',
start='1968-12-31')
# convert daily to annual
gold_download = gold_download.resample('A').last().reset_index()
gold_download.set_index(pd.DatetimeIndex(gold_download['DATE']).year, inplace=True)
gold_download['return'] = gold_download['GOLDAMGBD228NLBM'].pct_change()
gold_download.to_csv('gold_fred.csv')
After some additional data-wrangling we have a dataframe df of real returns 1928-1999 for T-bills, T-notes, Baa corporate bonds, S&P, and gold (see the notebook).
To find the minimum-volatility portfolio:
import cvxpy as cp
# compute covariance matrix (df being the dataframe of historical returns)
Sigma = np.cov(df.transpose())
# number of assets
n = Sigma.shape[0]
# average returns
mu = df.mean().values
# asset SDs
asset_vols = np.sqrt(Sigma.diagonal())
# variable to optimize over - portfolio weights
w = cp.Variable(n)
# objectives to optimize
# portfolio return
ret = mu.T @ w
# volatility
vol = cp.quad_form(w, Sigma)
prob = cp.Problem(cp.Minimize(vol), # minimize volatility
[cp.sum(w) == 1, # sum of weights = 1
w >= 0] # weights > 0 (long-only)
)
prob.solve()
wts = [float('%0.4f' % v) for v in w.value]
minvol = vol.value
Now we have the leftmost point on the efficient frontier. The rightmost point is the highest possible return we could have achieved, which is 100% in the highest-performing asset. We know it’s the S&P but let’s let CVXPY figure it out for us:
# Solve max return portfolio (corner solution)
prob = cp.Problem(cp.Maximize(ret), # maximize return
[cp.sum(w) == 1,
w >= 0]
)
prob.solve()
wts = [float('%0.4f' % v) for v in w.value]
maxretvol = vol.value
Finally, we trace out the rest of the frontier. We create an array of 200 volatilities between minvol and maxretvol inclusive. For each volatility, we solve the optimization for the highest return portfolio subject to volatility <= vol:
vol_limit = cp.Parameter(nonneg=True)
prob = cp.Problem(cp.Maximize(ret),
[cp.sum(w) == 1,
w >= 0,
vol <= vol_limit # new constraint: vol <= vol_limit parameter
]
)
# define helper function
def solve_vl(vl_val):
vol_limit.value = vl_val
result = prob.solve()
return (ret.value, np.sqrt(vol.value), w.value)
# number of points on the frontier
NPOINTS = 200
vl_vals = np.linspace(minvol, maxretvol, NPOINTS)
# iterate over vl_vals
results_dict = {}
for vl_val in vl_vals:
results_dict[vl_val] = solve_vl(vl_val)
Then we draw the frontier with matplotlib (same chart as at the top of this post):

And the transition map:

This covers a very long timespan. Let’s look at 1972-2019, i.e. after the US abandoned the gold standard:
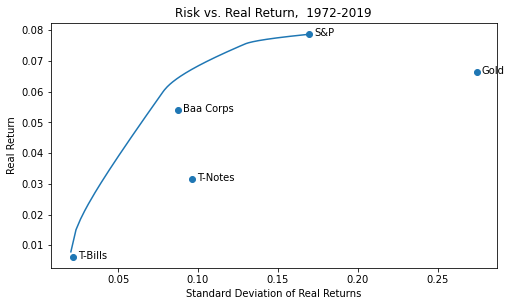

In this more inflationary period, somewhat more gold would have been optimal.
Finally, let’s look at 1983-2018, i.e. the era of disinflation (compare the gold marker vs. the previous chart):
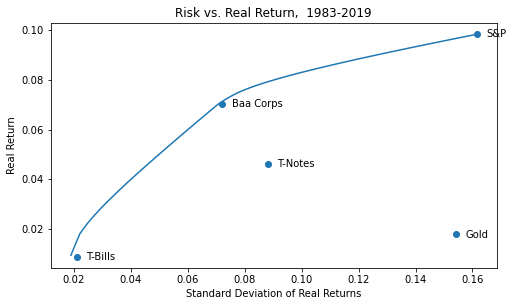
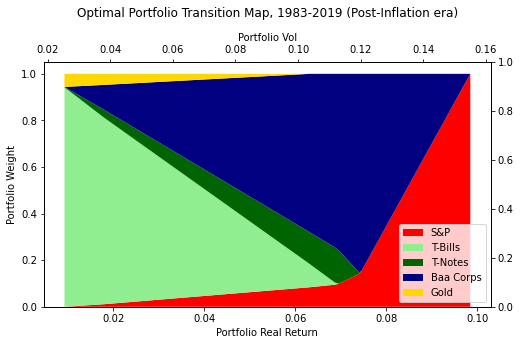
Gold added value in the most inflationary period, but is present even in the last period. I would argue that the question is not whether you should have some inflation hedge in your portfolio but if you should have gold or something else, like TIPS, Bitcoin, leveraged real estate.
Long-short optimization
To illustrate CVXOPT for a long-short portfolio, we create a synthetic asset that returns -5% per year and has 0.9 correlation with the S&P, which we called ‘stonks’. We remove the constraint of weights being positive but add a constraint that the gross exposure must be less than 150%:
vol_limit = cp.Parameter(nonneg=True)
prob = cp.Problem(cp.Maximize(ret),
[cp.norm1(w) <= 1.5, # 1-norm <= 1.5, i.e. gross exposure < 150%
cp.sum(w) == 1,
vol <= vol_limit]
)
# define function so we can solve many in parallel
def solve_vl(vl_val):
vol_limit.value = vl_val
result = prob.solve()
return (ret.value, np.sqrt(vol.value), w.value)
# number of points on the frontier
NPOINTS = 200
vl_vals = np.linspace(minvol, maxretvol, NPOINTS)
# iterate in-process
results_dict = {}
for vl_val in vl_vals:
results_dict[vl_val] = solve_vl(vl_val)
On the efficient frontier, for the same risk as stocks, you get a much higher return, or you get an equal return to stocks at about half the risk. Blinding glimpse of the obvious: if you can find good shorts and use leverage, you can supercharge returns. Note that the transition map visualizes gross exposures, but the stonks and occasionally some of the other assets go short.
Factor model
As a final CVXOPT example, we can create a set of random factors and stocks with random exposures to these factors and random returns, and solve for the minimum-volatility portfolio and an efficient frontier:
# number of stocks
n = 1000
# random historical mean returns for each stock
mu = np.random.normal(0.1, 0.2, n)
# number of factors
m = 10
# factor covariance matrix - random symmetrical matrix
SigmaFactor = np.random.randn(m, m)/4
SigmaFactor = SigmaFactor.T @ SigmaFactor
# factor loadings, determine volatility and covariances between stocks
F = np.random.randn(n, m)
# idiosyncratic risk of each stock
D = np.diag(np.random.uniform(0, 0.9, size=n))
ret = mu.T @ w # solve for weights that maximize portfolio return
f = F.T @ w # portfolio factor loading
Lmax = cp.Parameter() # leverage constraint
Lmax.value = 2
# portfolio volatility: factor risk + idiosyncratic risk
risk = cp.quad_form(f, SigmaFactor) + cp.quad_form(w, D)
prob = cp.Problem(cp.Minimize(risk),
[cp.sum(w) == 1,
cp.norm(w, 1) <= Lmax])
prob.solve(solver=cp.OSQP)
minvol = risk.value
minvolret = ret.value
print("Min vol portfolio (return=%.4f, risk=%.4f)" % (minvolret, minvol))
Concluding remarks
Mean-variance optimization is a useful framework. I think of markets as boundedly efficient, and I believe efficient-market maximalists have done investors a disservice by overselling modern portfolio theory. Beyond the forms of the efficient market hypothesis, even the weakest of which is only approximately true, here are 3 important fallacies (or at least oversimplifications) that sometimes get taught:
-
The risk-free rate and the capital market line. Suppose there is a risk-free rate with an SD of 0 and some positive return. If you draw a line on the efficient frontier chart, starting from the risk-free rate and tangent to the efficient frontier, it represents the highest feasible Sharpe ratio. You can maximize the Sharpe ratio by holding the market portfolio at the tangent point, and the risk-free asset in some combination, choosing your desired level of risk and return. Similarly, if you can borrow at some rate you can lever up the max-Sharpe portfolio to achieve the highest possible Sharpe at higher levels of risk. It follows that everyone should just hold something close to the market portfolio with varying degrees of leverage based on their risk tolerance. But in practice, there ain’t no such thing as a risk-free rate. If you are allocating for a timeframe greater than a few years, you should be focusing on real inflation-adjusted, after-tax returns, not nominal returns. In that context, there is no risk-free rate. And there can be no risk-free positive real rate in a real world subject to disasters and policy discontinuities. To expect markets or governments to ensure investors are guaranteed a positive real after-tax return, in a world of wars and pandemics, where participants in goods and labor markets receive no such guarantee, is a chimerical notion.
-
Betas (or factors) are all that matters. If you assume that factors capture all the correlations between stocks, then the unsystematic risk of one stock is always uncorrelated with the risk of other stocks, and furthermore, with a sufficient number of stocks, the unsystematic risk diversifies out. All that’s left is beta, the risk captured by the factors. In practice, this is a bad assumption, particularly at times of market stress. No factor model can never capture all the underlying real-world correlations and potential correlations, many of which are never realized. No model captures everything. The common factors that influence stock returns consistently over the long run, like GDP growth, don’t explain all the correlations, and the factors that would explain all the correlations would be numerous and change over time. For instance, if California tumbles into the sea, a lot of stocks that previously had low correlations will be highly correlated. Because, first of all, California exposure was not previously a factor but now suddenly is. And secondly because in a big market discontinuity correlations tend to go to one, and seemingly diversified portfolios become riskier than predicted. The discontinuity overwhelms everything else, traders trade what there is a market for and not what is specifically impacted by news flows, and betas tend not to sway them. The modeled risk of a portfolio should be viewed as a lower bound in a normal market where the present is like the past.
-
Everyone should hold the market portfolio because it is game-theory optimal. Granted, if you hold the market portfolio, and the market portfolio never changes, and you never need to trade, you are guaranteed the market return. But everyone has to trade sometime. Once you receive dividend or interest income to reinvest, or need to rebalance, or have any cash flows into or out of the portfolio, your returns depend on your trading efficiency and alignment with market timing. No one can be 100% passive. And when you have to trade, the sharks are waiting to exploit you. The smart money, like market-makers or Warren Buffett, can demand an explicit or implicit bid-ask by only giving the other side of the trade when it’s worth their while. Furthermore, when the index changes, you are forced to trade to match it, and people will front-run you. If Tesla goes into the S&P at $700/share as a top-10 market cap, and you are able to buy it at $700/share, you will match the index, but it doesn’t mean you didn’t get fleeced. The dominance of indexing assumes cost-free trading, and trading always costs money, sometimes a lot. In practice, the more investors index, the more inefficient the market gets, making it more costly to trade, and increasing the opportunity set for non-indexers. If you don’t have an edge, indexing and implicitly trying to tag along with the average investor is extremely sensible. But it is not guaranteed to be a free lunch. You have to trade as little as possible, and avoid buying at the top and selling at the bottom. Most retail investors don’t match the market for many reasons, some of which are neutralized by indexing. But even retail index investors underperform because they tend to buy and sell at the worst times.
I’m reminded of Donald Knuth, “Beware of bugs in the above code; I have only proved it correct, not tried it.” This maxim may apply to modern portfolio theory as well as to what I just wrote. Economics is the only discipline in which two academics can receive a Nobel Prize for research where they directly contradict each other (Fama and Shiller). Portfolio theory is a brilliant and useful map of reality, not reality itself. Navigating with excessive confidence on the basis of imperfect models can be taken to extremes where models lose some of their usefulness.
A desk is a dangerous place from which to view the world. – John Le Carré
-
For a more mathematical explanation, suppose market returns, expressed as sequential changes in log, follow a normal distribution, and market prices therefore follow a lognormal distribution. The daily volatility maps directly to long-run volatility, because long-run log diffs are the sum of daily log diffs. So short-run volatility tells you long-run volatility over your investing time frame, which is risk. Risk means that over your investment horizon, say 10 years, the investment could do very well or very poorly; that distribution of returns defines your risk. If you know the volatility of daily returns, you can infer the volatility of 10-year returns and vice versa. For normally distributed returns, you can annualize volatility following a square-root-of-time law. Modulo serial correlation, the annualized daily volatility will match the annualized 10-year volatility. (It seems reasonable that quant or trend traders would largely arb out any systematic serial correlation.) Note that stock returns do not exactly follow a normal distribution, they have fatter tails, especially on the left. Entropy means it’s easier to have a negative shock than a positive one: you can instantaneously implode a skyscraper but you can’t instantaneously build one. Similarly you can have a market meltdown but typically not a melt-up. Maybe an appropriate distribution is a combination of a normal distribution and a Poisson distribution for rare shocks. But that’s getting into the weeds, the point is that short-run volatility is a useful proxy for longer-term risk. ↩
-
We reverse the sign because of the inconvenient convention of how triangle angles are measured. Suppose you start walking in the direction of segment \(a_1\) for the first asset. If for segment \(a_2\) you keep going in the same direction, that corresponds to \(\alpha'\) = 0°, correlation = 1.0. If you do a 180, that corresponds to \(\alpha'\) = 180°, correlation = -1.0. If you make a right-angle turn in either direction, that corresponds to \(\alpha'\) = +/- 90°, correlation = 0. The way we usually measure triangle angles, an angle of 0 corresponds to doing a 180, which is a slightly backwards way of looking at it. So we have to reverse the sign on the classic cosine rule to make cosine math correspond to correlation math. But the spatial relationship is the same. ↩