How much can you safely spend out of a portfolio in retirement? Spend conservatively and you may be unnecessarily curbing the lifestyle and aspirations of you and your loved ones. Overspend and risk a shortfall and painful adjustment - in the extreme, the (hopefully apocryphal) “cat food” diet. A traditional rule of thumb is a fixed 4% per year of your starting portfolio, adjusted each year for inflation. A previous post discussed why this rule may not be safe:

  • Low bond yields _ 1.8% for 10-year Treasurys and negative TIPS out to 10 years _ mean historical bond returns are mathematically unobtainable.1
  • 2.2% real returns since 2000 on a 60/40 blended portfolio suggest that long-run return expectations need to be revisited. Low long-term interest rates are a forecast of low future returns, ie low growth and inflation expectations. To the extent equity risk premiums haven’t widened, they forecast lower than normal equity returns.
  • Taxes and investment expenses must be included. Work supporting 4% tends to ignore them.
  • US demographics are not very positive for growth, inflation, tax rates, and hence, real after-tax investment returns (which is reflected in the US fiscal position). The US dependency ratio is forecast to rise by 15 points over the next 20 years.

If the 4% rule hasn’t been decisively breached, forward-looking indicators are a bit worrisome. Could a more flexible rule not only be safer, but in favorable circumstances allow a higher level of spending? In this 3-part post, we test dynamic rules that vary withdrawal rates based on age and the size of the portfolio, and vary the composition of the portfolio over time.

Dynamic rule 1: Vary spending by age.

The first rule we’ll test is to spend a percentage of the actual portfolio each year (not a fixed percentage of the initial portfolio) and vary the percentage by age.

Suppose you are a 65 year old male. You have a life expectancy of 17.19 years per US government actuarial tables. It would make sense to vary spending as a percentage of your assets inversely with your life expectancy. As a base case you could spend 1/17.19=5.82% of your portfolio this year. Next year your life expectancy would be 16.48% You would spend 1/16.48=6.07%. This is higher than 4% for life expectancy < 25 years, but it’s an arbitrary base case _ just a starting point to test a rule based on the size of the portfolio and life expectancy.

Let’s apply this rule to a 60/40 stock/bond portfolio for someone who retired in 1928 to and see what spending it would have supported.

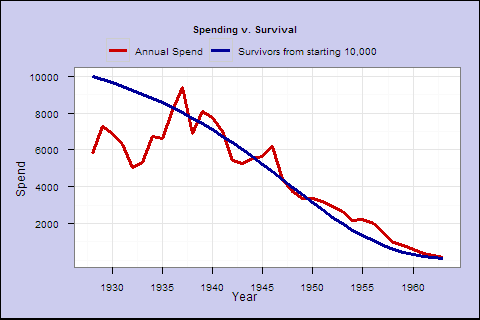
Figure 1. Inflation-adjusted spending for a 65-year-old single male who retires in 1928, with dynamic spending rule of 1/life_expectancy (spending factor=1) v. survival rate

Income v. Survival, 1928 males, 60/40 portfolio, spending factor 1

This retiree would have experienced volatility, but he would really have started to go broke after around 1947, aged 85, shortly after his original life expectancy at retirement. From the blue survival line (from current life expectancy tables), over 40% would still have been alive for that drop. If he lived to be 100 after 35 years in 1963, he would have been penniless.

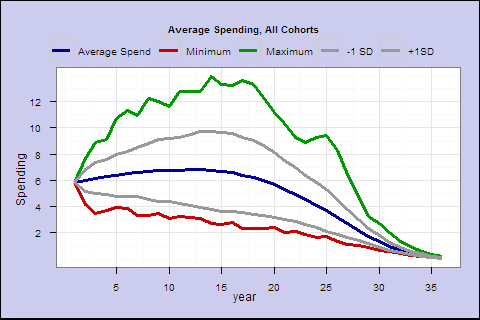
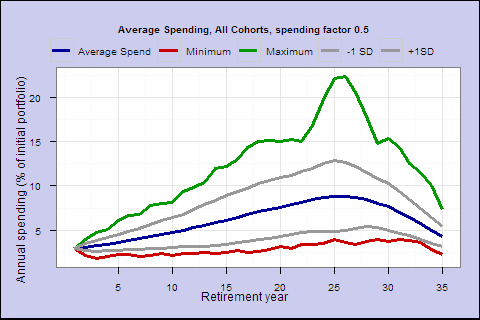
Is this rule too spendthrift, or was 1928 a particularly bad year to start retirement? Let’s try the same rule in all available 35-year retirement cohorts 1928-1977, and plot their average spending.

Figure 2. Average spending, 60/40 portfolio, spending factor 1, retirement age 65, all cohorts

Average spending, 60/40 portfolio, spending factor 1, retirement age 65, all cohorts

The middle blue line is the average income by retirement year. The green and red are the best and worst cases. The middle 2 lines represent the +/- 1 standard deviation confidence interval.

Even in the best case, you eventually go broke. Your life expectancy is 17.2 years at retirement, and on average your spending goes below the starting amount around year 19. This spending rule may not conservative enough.

Let’s call s spending factor, and try different spending rates s/life_expectancy. We can run spending factors between 0.05 and 1.2: Figure 3. Big chart panel (opens in new window). As we move toward the top of the page, we see safer profiles, and even the worst case scenarios start to seem fairly acceptable.

This exercise demonstrates the tradeoff between spending, and the risk of the average or worst-case income path exhibiting a major shortfall from the starting income.

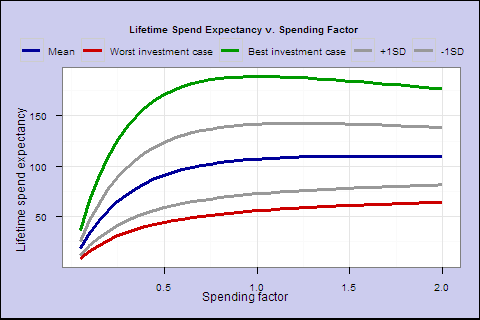
To better visualize this big panel, we can estimate ‘lifetime spend expectancy’ and shortfall probability for each spending factor.

Figure 4. Lifetime spending expectancy (% of initial portfolio) v. spending factor

Lifetime spend expectancy v. spending factor

In Figure 4, for each year, we multiply the spending outcome by the probability of a cohort retiree surviving to that year, and sum up the years, to get the lifetime spend expectancy for a given spending factor. This summarizes each line in the Figure 3 panel as a single point, the expected lifetime spending as a percentage of starting portfolio.

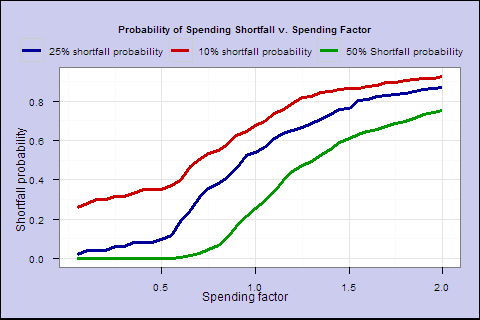
Figure 5. Probability of spending shortfall v. spending factor.

Probability of spending shortfall v. spending factor

In Figure 5, for each s, we calculate the percentage of retirees in all cohorts who survived to a year where the spending falls to 25% below the initial spending.

These last 2 charts illustrate that as you increase the spending factor past 0.6, increasing lifetime spend expectancy flattens out, and the probability of 25% shortfall accelerates sharply.

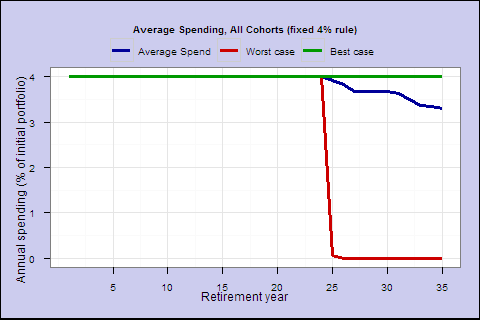
Finally, how does the fixed 4% rule compare? For a 65-year-old with a 60/40 portfolio, the 4% rule yields 70.4 expected lifetime spending with a 2% lifetime shortfall probability.

By comparison, a 0.5 spending factor, which starts at about 3% spending, yields expected spending of 91.2 with a 9.7% probability of a 25% drop from the initial spend amount, and a worst case drop of 37% (for 1973 retirees _ they eventually recovered).

But you do start at a lower rate, and spending is variable.

Figure 6. Average spending by retirement year, all cohorts, spending factor 0.5.

Average spending, all cohorts, spending factor 0.5

Figure 7. Average spending by retirement year, all cohorts, fixed 4% rule

Average spending by retirement year, all cohorts, Fixed 4% rule
In the next post, we’ll test additional rules, to vary the composition of the portfolio by age, and to try smooth spending.


1The objection has been made that today’s rates can go lower and bond returns can be higher in the short run. True, but a 10-year bond bought at a yield of 1.8% will return, best case, 1.8% nominal over its lifetime (less in the event of default). If the yield goes to zero this year, it will return 18% this year, and zero over the rest of its lifetime. It’s called “fixed” income for a reason. When interest rates are below inflation, thinking bonds can be a real total return instrument in the base case is setting up for disappointment. It hasn’t been true historically, and it’s not what the market is pricing in. Bonds still have an important role as a liquidity and deflation hedge.

?View Code RSPLUS 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329

ageframe <- function (lifetable, age, maxage)
{
    start = age+1
    end=maxage+1
    keep <- c("Age","Mmort","Mlives","MLE")
    retframe = lifetable[start:end,keep]
    retframe$survivepct=retframe$Mlives/retframe[1,"Mlives"]
    return(retframe)
}
 
cohortframe <- function (ageframe, portframe, startyear)
{
    retframe <-ageframe
    retireyears=nrow(ageframe)
    endyear = startyear+retireyears-1
    retframe$portreturn = portframe[startyear:endyear,"portreturn"]
    retframe$year = portframe[startyear:endyear,"Year"]
    return(retframe)
 
}
 
calcspending <- function(cohortframe, spendingfactor)
{
    retframe <- cohortframe
    retframe$spend=
    retframe$startportval=
    retframe$endportval=
    portval=100
    for (index in 1: nrow(retframe)) {
        myrow = retframe[index,]
        myrow["startportval"]=portval
        spendrate = spendingfactor/myrow["MLE"]
        spend = spendrate * portval
        myrow["spend"]=spend
        portval = portval - spend
        portval = portval * (1 + myrow["portreturn"])
        myrow["endportval"]=portval
        retframe[index,]=myrow
    }
    return(retframe)
}
 
calcspendingfixed <- function(cohortframe, spendingfactor)
{
    retframe <- cohortframe
    retframe$spend=
    retframe$startportval=
    retframe$endportval=
    portval=100
    for (index in 1: nrow(retframe)) {
        myrow = retframe[index,]
        myrow["startportval"]=portval
        if ( portval > 4) {
            spend = 4
        } else {
            spend <- portval
        }
        myrow["spend"] <- spend
 
        portval = portval - spend
        portval = portval * (1 + myrow["portreturn"])
        myrow["endportval"]=portval
        retframe[index,]=myrow
    }
    return(retframe)
}
 
testspendingfactor <- function(realreturns, spendingfactor, minage, maxage)
{
    tempageframe <- ageframe(lifetable, minage, maxage)
    ntrials <- nrow(realreturns)-nrow(tempageframe) +1
    nyears <- maxage-minage+1
    trials <- data.frame(1:nyears)
    colnames(trials) = "age"
    for (index in 1:ntrials) {
        tempframe1 = cohortframe(tempageframe,realreturns,index)
        tempframe2 = calcspending(tempframe1,spendingfactor)
        colname = paste("trial",index, sep="")
        trials[colname] <- tempframe2$spend
    }
 
    trials <- trials[2:ncol(trials)]
    return(trials)
 
}
 
testspendingfactorfixed <- function(realreturns, spendingfactor, minage, maxage)
{
    tempageframe <- ageframe(lifetable, minage, maxage)
    ntrials <- nrow(realreturns)-nrow(tempageframe) +1
    nyears <- maxage-minage+1
    trials <- data.frame(1:nyears)
    colnames(trials) = "age"
    for (index in 1:ntrials) {
        tempframe1 = cohortframe(tempageframe,realreturns,index)
        tempframe2 = calcspendingfixed(tempframe1,spendingfactor)
        colname = paste("trial",index, sep="")
        trials[colname] <- tempframe2$spend
    }
 
    trials <- trials[2:ncol(trials)]
    return(trials)
}
 
calctrialssummary <- function(trials)
{
    trialssummary <- data.frame(1:nrow(trials))
    colnames(trialssummary) = "year"
    trialssummary$mean=apply(trials,1,mean)
 
    trialssummary$max=apply(trials,1,max)
    trialssummary$min=apply(trials,1,min)
    trialssummary$sd=apply(trials,1,sd)
    trialssummary$plus1sd=trialssummary$mean + trialssummary$sd
    trialssummary$minus1sd=trialssummary$mean - trialssummary$sd
    keep <- c("year", "mean","min","max","minus1sd","plus1sd")
    trialssummary <- trialssummary[,keep]
 
    return(trialssummary)
}
 
 
calcexpectedspending<- function(trials, survival)
{
    trialssummary <- data.frame(1:nrow(trials))
    colnames(trialssummary) = "year"
 
    trialssummary$survivepct=survival$survivepct
    trialssummary$mean=apply(trials,1,mean)
    trialssummary$expmean= trialssummary$mean * trialssummary$survivepct
    trialssummary$max=apply(trials,1,max)
    trialssummary$expmax= trialssummary$max * trialssummary$survivepct
    trialssummary$min=apply(trials,1,min)
    trialssummary$expmin= trialssummary$min * trialssummary$survivepct
    trialssummary$sd=apply(trials,1,sd)
    trialssummary$plus1sd=trialssummary$mean + trialssummary$sd
    trialssummary$expplus1sd= trialssummary$plus1sd * trialssummary$survivepct
    trialssummary$minus1sd=trialssummary$mean - trialssummary$sd
    trialssummary$expminus1sd= trialssummary$minus1sd * trialssummary$survivepct
 
    keep <- c("year", "expmean","expmin","expmax", "expplus1sd", "expminus1sd")
    trialssummary <- trialssummary[,keep]
    return(trialssummary)
}
 
chartsummary <- function(trialssummary, mytitle)
{
    meltframe <- melt(trialssummary, id = 'year')
    ggplot(data=meltframe, aes(x=year, y=value, colour=variable)) +
     scale_x_continuous() +
     ylab("Annual spending (% of initial portfolio)") +
     xlab("Retirement year") +
     theme_bw() +
     geom_line(size=1.4) +
     opts(legend.position="top",
          legend.direction = 'horizontal',
          plot.background = theme_rect(colour = 'black', fill = '#CCCCEE', size = 1, linetype='solid')) +
     scale_colour_manual(mytitle, breaks = c('mean', 'min','max','minus1sd','plus1sd'),
                         values = c("#000099", "#CC0000","#009900","#999999","#999999"),
                        labels = c('Average Spend', 'Minimum', 'Maximum', '-1 SD', '+1SD'))
}
 
library(ggplot2)
 
returns <- read.csv("~/Documents/returns.csv")  # /assets/wp-content/uploads/2013/01/returns.csv
lifetable <- read.csv("~/Documents/Lifetable.csv") # /assets/wp-content/uploads/2013/01/Lifetable.csv
 
returns$realstocks=returns$Stocks-returns$CPI
returns$realbonds=returns$Bonds-returns$CPI
returns$realbills=returns$Bills-returns$CPI
 
drops <- c("Stocks","Bonds","Bills","CPI")
realreturns <- returns[,!(names(returns) %in% drops)]
realreturns$portreturn = 0.6*realreturns$realstocks + 0.4 *realreturns$realbonds
 
#Figure 1
 
tempageframe <- ageframe(lifetable, 65, 100)
tempframe1 = cohortframe(tempageframe,realreturns,1)
tempframe2 = calcspending(tempframe1,1)
tempframe2$survival65 = tempframe2$survivepct * 10000
tempframe2$spend = tempframe2$spend * 1000
keep = c("year","spend","survival65" )
tempframe2 <- tempframe2[,keep]
meltframe <- melt(tempframe2, id = 'year')
 
ggplot(data=meltframe, aes(x=year, y=value, colour=variable)) +
     scale_x_continuous() +
     ylab("Spend") +
     xlab("Year") +
     theme_bw() +
     geom_line(size=1.4) +
     opts(legend.position="top",
          legend.direction = 'horizontal',
          plot.background = theme_rect(colour = 'black', fill = '#CCCCEE', size = 1, linetype='solid')) +
     scale_colour_manual("Annual spending, retirement age 65, 60/40 portfolio, spending factor 1, 1928 cohort", breaks = c('spend', 'survival65'),
                         values = c("#CC0000", "#000099"),
                        labels = c('Annual Spend', 'Survivors from starting 10,000'))
 
 
#Figure 2
trials = testspendingfactor(realreturns, 1, 65, 100)
trialssummary = calctrialssummary(trials)
trialssummary$survival = ageframe65$survivepct*10000
keep <- c("year", "mean","min","max","minus1sd","plus1sd")
trialssummary <- trialssummary[,keep]
chartsummary(trialssummary, "Average Spending, All Cohorts")
 
 
# Figure 3
facetframe = data.frame (year = integer(), variable=character(), value=double())
 
for (index in 1:24) {
    spendingfactor = index/20
    trials = testspendingfactor(realreturns, spendingfactor, 65, 100)
    trialssummary = calctrialssummary(trials)
    trialssummary$spendingfactor = spendingfactor
    meltframe <- melt(trialssummary, id = c('year','spendingfactor'))
    facetframe <- merge(meltframe, facetframe, all=TRUE)
}
 
ggplot(data=facetframe, aes(x=year, y=value, colour=variable)) +
    scale_x_continuous() +
    ylab("Annual spending (% of initial portfolio)") +
    xlab("Retirement year") +
    theme_bw() +
    facet_wrap(~ spendingfactor, ncol = 4) +
    geom_line(size=1) +
    opts(legend.position="top",
         legend.direction = 'horizontal',
         plot.background = theme_rect(colour = 'black', fill = '#CCCCEE', size = 1, linetype='solid')) +
scale_colour_manual("Average Spending, All Cohorts, Spending Factors 0.05 to 1.2", breaks = c('mean', 'min','max','minus1sd','plus1sd'),
                    values = c("#000099", "#CC0000","#009900","#999999","#999999"),
                    labels = c('Average Spend', 'Minimum', 'Maximum', '-1 SD', '+1SD'))
 
############################################################
 
 
ageframe65 = ageframe(lifetable,65,100)
nsfactors = 40
sfactorsummary <- data.frame(1:nsfactors)
colnames(sfactorsummary) = "year"
sfactorsummary$sfactor <- 
sfactorsummary$expspend <- 
sfactorsummary$minspend <- 
sfactorsummary$maxspend <- 
sfactorsummary$plus1sd <- 
sfactorsummary$minus1sd <- 
sfactorsummary$sdspend <- 
sfactorsummary$shortfall <- 
 
for (index in 1:nsfactors) {
    spendingfactor = index/20
    trials = testspendingfactor(realreturns, spendingfactor, 65, 100)
    trialssummary = calcexpectedspending(trials, ageframe65)
 
    sfactorsummary$sfactor[index] = spendingfactor
    sfactorsummary$expspend[index] = sum(trialssummary[,"expmean"])
    sfactorsummary$minspend[index] = sum(trialssummary[,"expmin"])
    sfactorsummary$maxspend[index] = sum(trialssummary[,"expmax"])
    sfactorsummary$plus1sd[index] = sum(trialssummary[,"expplus1sd"])
    sfactorsummary$minus1sd[index] = sum(trialssummary[,"expminus1sd"])
    sfactorsummary$sdspend[index]=rowMeans(apply(trials, 2, sd)/trials[1,])
 
    trialstmp=trials
    for (index2 in 1:ncol(trialstmp))
        trialstmp[index2]=trialstmp[index2]/trialstmp[1,index2]
    trialstmp[trialstmp<0.75]=-1
    trialstmp[trialstmp>]=
    trialstmp[trialstmp<]=1
    for (index2 in 1:ncol(trialstmp))
        trialstmp[index2]=trialstmp[index2] * ageframe65$survivepct
    sfactorsummary$shortfall[index]=mean(apply(trialstmp,2,max))
}
 
 
chart1=sfactorsummary
keep <- c("sfactor","expspend","minspend","maxspend","plus1sd","minus1sd")
chart1 <- chart1[keep]
 
meltframe <- melt(chart1, id = 'sfactor')
 
ggplot(data=meltframe, aes(x=sfactor, y=value, colour=variable)) +
    scale_x_continuous() +
    ylab("Lifetime spend expectancy (% of initial portfolio)") +
    xlab("Spending factor") +
    theme_bw() +
    geom_line(size=1.4) +
    opts(legend.position="top",
         legend.direction = 'horizontal',
         plot.background = theme_rect(colour = 'black', fill = '#CCCCEE', size = 1, linetype='solid')) +
scale_colour_manual("Lifetime Spend Expectancy v. Spending Factor", breaks = c('expspend', 'minspend','maxspend','plus1sd','minus1sd'),
                    values = c("#000099", "#CC0000", "#009900","#999999","#999999"),
                    labels = c('Mean', 'Worst investment outcome', 'Best investment outcome','+1SD','-1SD'))
 
chart2=sfactorsummary
keep <- c("sfactor","shortfall")
chart2 <- chart2[keep]
meltframe <- melt(chart2, id = 'sfactor')
 
ggplot(data=meltframe, aes(x=sfactor, y=value, colour=variable)) +
    scale_x_continuous() +
    ylab("Shortfall probability") +
    xlab("Spending factor") +
    theme_bw() +
    geom_line(size=1.4) +
    opts(legend.position="top",
         legend.direction = 'horizontal',
         plot.background = theme_rect(colour = 'black', fill = '#CCCCEE', size = 1, linetype='solid')) +
scale_colour_manual("Probability of 25% Spending Shortfall v. Spending Factor", breaks = c('shortfall'),
                    values = c("#000099"),
                    labels = c('Shortfall probability'))
 
 
# fixed 4% rule
trials = testspendingfactorfixed(realreturns, 1, 65, 100)
trialssummary = calctrialssummary(trials)
ageframe65 = ageframe(lifetable,65,100)
trialssummary$survivepct=ageframe65$survivepct
trialssummary$expmean = trialssummary$mean * trialssummary$survivepct
sum(trialssummary$expmean)
 
trials[trials<4]=-1
trials[trials>]=
trials[trials<]=1
trials[,]=trials[,] * ageframe65$survivepct
mean(apply(trials,2,max))
 
# 0.5 spending factor -> look up from sfactorsummary